Effet Gibbs-Donnan

Définition

L'effet Gibbs-Donnan décrit l'équilibre qui intervient entre deux solutions contenant des particules chargées (ions ou molécules chargées) lorsqu'elles sont séparées par une membrane. À cet équilibre, la membrane est sélectivement perméable à certaines particules chargées contenues dans les solutions (semi-perméabilité). Habituellement, les grosses particules ne sont pas autorisées à passer.

L'effet Gibbs-Donnan est le comportement des particules chargées à travers une membrane semi-perméable. Parce que certaines particules ne peuvent pas diffuser à travers la membrane (protéines), leur présence électrostatique entraînera la distribution asymétrique des ions perméables.

Schéma d'un équilibre passif de Gibbs-Donnan :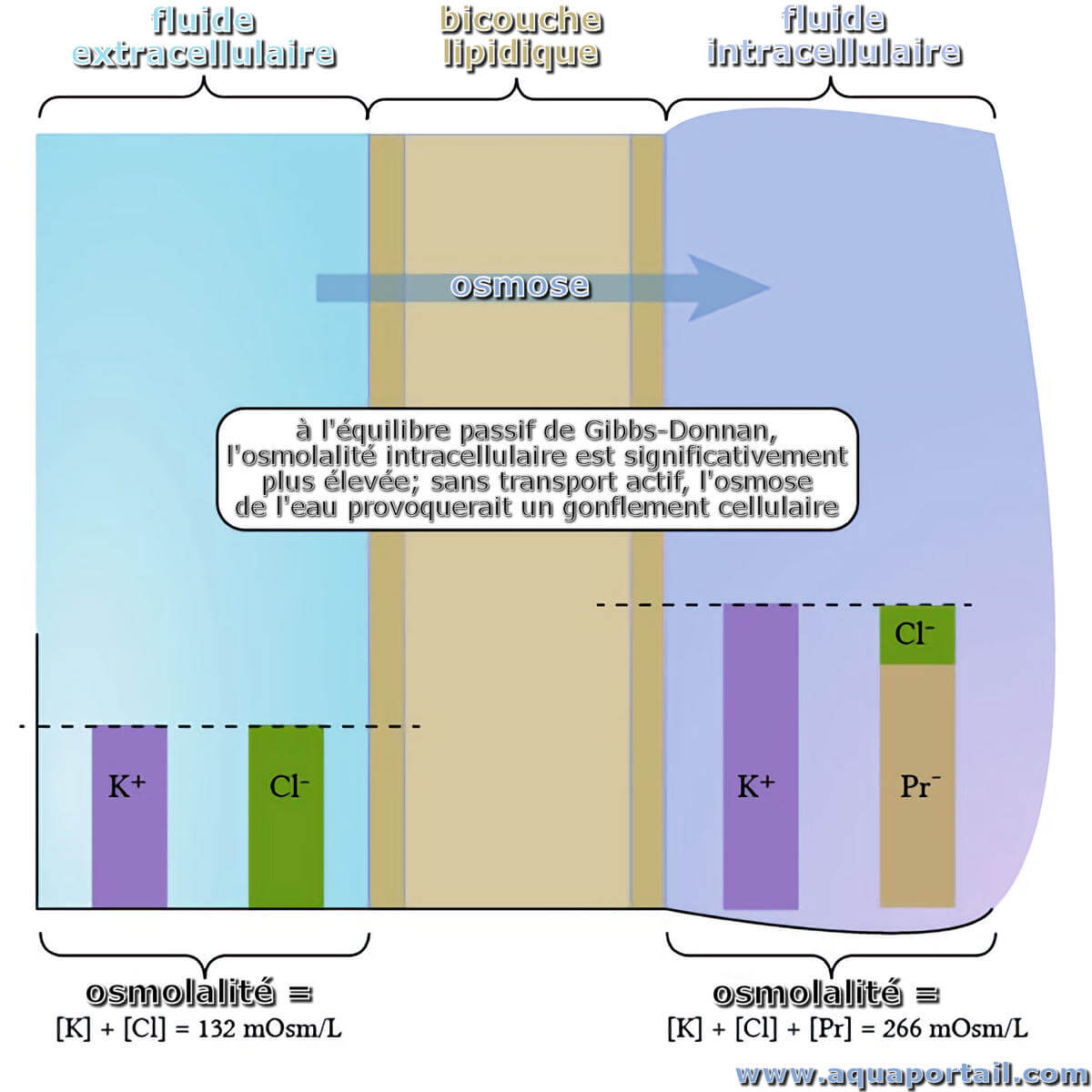

À l'équilibre de Gibbs-Donnan (passif), l'osmolalité intracellulaire est significativement plus élevée; sans transport actif, l'osmose de l'eau provoquerait un gonflement cellulaire. Ici, une expérience avec du potassium substitué au sodium.

Explications

Une conséquence de la perméabilité sélective de la membrane est l'émergence d'un potentiel électrique, exprimé en mV, sur les deux côtés de la membrane (le potentiel Donnan). Les deux solutions varieront également en pression osmotique π, exprimée en Pa, par la différence de concentration ionique.

L'équilibre de Gibbs-Donnan existe typiquement une protéine chargée et une membrane de dialyse.

L'effet Gibbs-Donnan n'est bien sûr pas vraiment un mécanisme de transport à travers les membranes cellulaires; plutôt, le transport à travers les membranes cellulaires est le mécanisme de l'effet Gibbs-Donnan; mais de telles objections sont inutilement académiques.

L'effet d'équilibre porte le nom de l'Américain Josiah Willard Gibbs (1839–1903) et de l'Irlandais Frederick George Donnan (1870–1956). Donnan a donné une description du phénomène (loi de Donnan) en 1911.

Équilibre de Donnan

Le modèle d'équilibre de Donnan tient compte de la charge du soluté et de la charge membranaire qui, par répulsion des co-ions et attraction des contre-ions, crée un potentiel de Donnan à la surface de la membrane. Cela a pour effet de repousser les co-ions et, l'électroneutralité devant être préservée, les contre-ions sont également rejetés.

Imperméant

Est imperméant ce qui est imperméable à certains ions ou molécules chargées. Par exemple, une paroi imperméante ne laisse pas un fluide la traverser : elle est imperméable à certaines molécules.

Mécanismes d'équilibre

L'effet Gibbs-Donnan décrit la distribution inégale des ions chargés de perméation de chaque côté d'une membrane semi-perméable qui intervient en présence d'ions chargés imperméants.

À l'équilibre de Gibbs-Donnan :

• De chaque côté de la membrane, chaque solution sera électriquement neutre;
• Le produit des ions diffusibles d'un côté de la membrane sera égal au produit des ions diffusibles de l'autre côté de la membrane;
• Les gradients électrochimiques produits par une distribution inégale des ions chargés produisent une différence de potentiel transmembranaire qui peut être calculée à l'aide de l'équation de Nernst;
• La présence d'ions imperméables d'un côté de la membrane crée un gradient de diffusion osmotique attirant l'eau dans ce compartiment.

Les mécanismes qui maintiennent le potentiel membranaire au repos et les mécanismes de l'effet Gibbs-Donnan sont des phénomènes différents :

• L'équilibre de Donnan est un processus complètement passif : c'est-à-dire qu'aucun transporteur actif n'intervient dans le maintien de cet équilibre;
• Un équilibre de Donnan est un équilibre, c'est-à-dire que les concentrations d'ions de part et d'autre de la barrière sont statiques;
• Si l'équilibre de Donnan devait s'établir complètement, l'augmentation des ions intracellulaires ferait gonfler les cellules en raison de l'afflux osmotique d'eau;
• À un équilibre de Donnan, le potentiel de membrane au repos ne serait que d'environ -20 mV. Ce potentiel existerait même si la perméabilité de la membrane pour tous les ions était la même;
• Le potentiel membranaire au repos, en revanche, nécessite des perméabilités différentes pour le potassium et pour le sodium, et est maintenu activement par une activité Na⁺/K⁺ ATPase constante;
• Parce que les membranes biologiques (en particulier des tissus excitables) ne sont jamais à l'équilibre, l'équation de Goldman-Hodgkin-Katz est généralement un meilleur choix pour expliquer leur comportement électrochimique.

Exemple avec du potassium substitué au sodium

L'expérience simplifiée à deux compartiments reste un moyen efficace d'explication du concept; ajouter du réalisme cellulaire à cette description sacrifierait la clarté à la précision.

Voici ces deux compartiments. Dans le but de maintenir un certain attachement aux documents du programme des collèges, étiquetons-les "intracellulaires" et "extracellulaires". Dans ces compartiments, certains ions sont dissous. Faisons ces potassium et chlorure, parce que ceux-ci semblent importants. Une membrane sépare les compartiments. La membrane est quelque peu perméable (perméante) aux ions potassium et chlorure, mais complètement imperméable (imperméante) aux protéines.

La concentration d'électrolytes dans chaque compartiment est égale et l'électroneutralité de chaque compartiment est maintenue. Si l'on était dans cette voie, on pourrait peut-être représenter cet équilibre comme une équation, où "int" signifie intracellulaire et "ext" signifie extracellulaire : [K⁺]_ext x [Cl^-]_ext = [K⁺]_int x [Cl^-]_int.

Remplaçons maintenant le KCl dans le compartiment intracellulaire par un protéinate de potassium, c'est-à-dire une molécule où le potassium est accompagné d'une protéine chargée négativement (Pr^-) comme conjugué. La protéine n'est pas diffusible et ne participe donc pas à l'équation ci-dessus (c'est-à-dire que [Pr^-]_ext ne peut jamais être identique à [Pr^-]_int). Maintenant, les concentrations intracellulaires et extracellulaires de potassium restent les mêmes (et donc le potassium n'est pas enclin à diffuser n'importe où), mais il existe maintenant un gradient de concentration pour les ions chlorure. Disons que la concentration d'origine était de 100 mmol/L; le gradient de concentration est maintenant de 100 mmol/L à 0 mmol/L.

Donc, parce que la membrane est perméable aux ions chlorure et qu'il y a maintenant un gradient de concentration, certains des ions chlorure diffusent dans le compartiment intracellulaire. Par nécessité, ils sont accompagnés de quelques ions potassium, de sorte que l'électroneutralité est préservée.

Les ions chlorure sont également repoussés par la protéine chargée négativement dans le compartiment intracellulaire, et ainsi la majeure partie du chlorure reste du côté extracellulaire de la membrane.

Donc; l'électroneutralité est préservée. Il en va de même pour l'équilibre de concentration totale des ions diffusibles, de sorte que le produit des concentrations d'ions diffusibles extracellulaires est le même que le produit des concentrations d'ions diffusibles intracellulaires : [K⁺]_ext x [Cl^-]_ext = [K⁺]_int x [Cl^-]_int.

Sans tomber dans la complexité des équations quadratiques, il suffira de dire que si on partait de concentrations de 100 mmol/L de part et d'autre, une fois la protéine ajoutée on se retrouve avec environ 33 mmol/L de chlorure du côté intracellulaire, ainsi que 133 mmol/L de potassium; les molécules d'ions supplémentaires provenaient du liquide extracellulaire et, par conséquent, ce compartiment devient relativement pauvre en ions, avec environ 66,6 mmol/L de chaque espèce.

Maintenant, bien sûr, parce qu'il y a un gradient électrique ainsi qu'un gradient de diffusion chimique agissant sur les ions, il y aura une répartition légèrement inégale de la charge à travers la membrane, conduisant à une différence de potentiel. Il s'agit d'un concept familier discuté en détail dans le chapitre sur le potentiel de membrane au repos. Il suffira de dire que pour chaque ion l'équilibre entre le gradient de concentration et le gradient électrique est décrit par l'équation de Nernst, et la différence de potentiel totale à travers la membrane qui résulte de l'effet combiné de tous les mouvements ioniques peut être décrite par l'équation de Goldman-Hodgkin-Katz, en tenant compte du fait que pour chaque ion, la perméabilité de la membrane sera différente.

En bref, l'effet Gibbs-Donnan crée une différence de potentiel transmembranaire car la distribution des ions chargés à travers la membrane est inégale. Cette différence de potentiel est apparemment assez faible.

Nous sommes donc maintenant à l'équilibre de Gibbs-Donnan : les produits des concentrations d'ions diffusibles doivent être les mêmes des deux côtés, et de chaque côté de la membrane la neutralité électrique est préservée. Cependant, la présence de protéines non diffusibles rend la concentration totale de molécules intracellulaires bien supérieure à la concentration de molécules extracellulaires :concentration intracellulaire = [K⁺]_int + [Cl^-]_int + [Pr^-]_int, et concentration extracellulaire = [K⁺]_ext + [Cl^-]_ext.

En fait, dans cette expérience de pensée (extrêmement inexacte sur le plan physiologique), la différence d'osmolalité est assez frappante (il y a environ 134 mOsm/L de différence). Avec ce type de gradient osmotique, l'eau jaillirait à travers la membrane, provoquant un gonflement affreux et une explosion de la cellule.

Évidemment, cela n'intervient pas in vivo. La Na⁺/K⁺ ATPase joue un rôle majeur dans la prévention de l'osmoexplosion cellulaire en pompant trois ions sodium hors de la cellule en échange de deux potassium. La terrible perméabilité au sodium de la membrane cellulaire fait que le sodium reste généralement dans le compartiment extracellulaire, y maintenant l'osmolalité.

En conséquence, un deuxième effet Donnan (cette fois avec les ions non diffusibles étant du sodium extracellulaire) est établi à travers la membrane, qui maintient un contre-gradient osmotique pour le mouvement de l'eau. Ainsi, il y a un "double effet Donnan" en action au niveau de chaque membrane cellulaire.

Les pompes à sodium alimentées par l'ATP diminuent l'osmolalité intracellulaire en transportant activement le sodium hors du liquide intracellulaire.

L'importance de la Na⁺/K⁺ ATPase dans le maintien d'un volume cellulaire stable a été bien établie par une série d'auteurs précoces qui ont désactivé la pompe en utilisant diverses méthodes et ont ensuite observé le gonflement et la rupture des cellules.

En rapport avec "effet Gibbs-Donnan"

• osmolalité

  

  L'osmolalité est une mesure de la concentration d'une solution qui représente le nombre d'osmoles par kilogramme de solvant.

• pression oncotique

  

  La pression oncotique, ou la pression osmotique colloïdale, est une forme de pression osmotique exercée par les protéines dans le plasma d'un vaisseau sanguin...

• pression osmotique

  

  La pression osmotique est une force déterminée par une différence de concentration entre deux solutions situées de part et d'autre d'une membrane...

• semi-perméable

  

  Une membrane semi-perméable est une membrane qui laisse passer le solvant mais pas le soluté, quoique cette semi-perméabilité ne soit pas aussi parfaite...