Polyèdre
Définition
Un polyèdre est, au sens donné par la géométrie classique, un corps géométrique dont les faces sont plates et renferment un volume fini. Les polyèdres sont conçus comme des corps tridimensionnels, mais il existe des topologies similaires du concept dans toutes les dimensions.
Plusieurs polyèdres :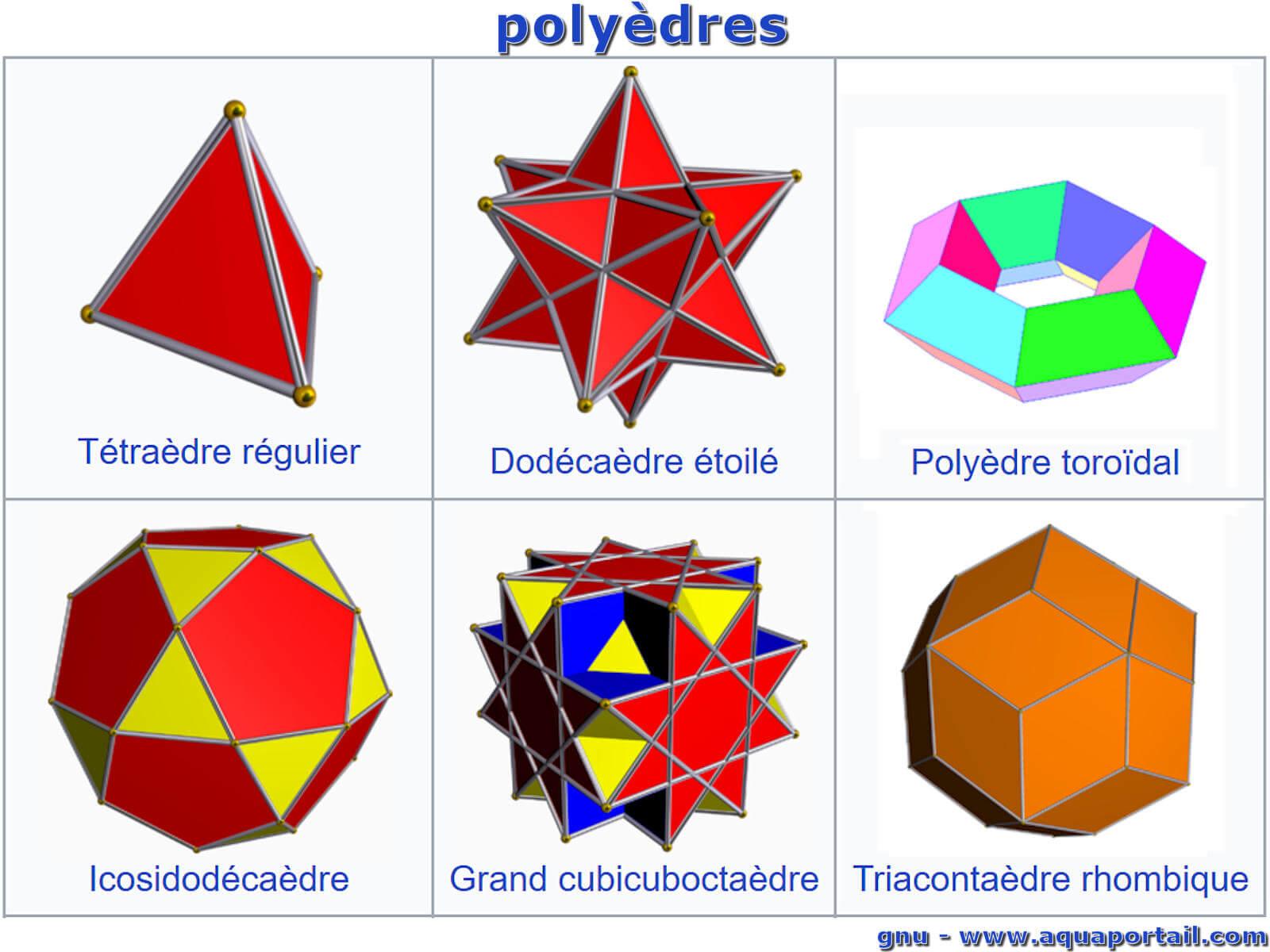
Les différents polyèdres sont (de gauche à droite et de haut en bas) : un tétraèdre régulier holoèdre, un dodécaèdre régulier, un polyèdre toroïdal, un icosidodécaèdre, un grand cubicuboctaèdre, un triacontaèdre rhombique.
Explications
Le point ou le sommet est la similarité topologique du polyèdre dans les dimensions nulles, une arête ou un segment dans une dimension, le polygone dans les deux dimensions. Le polychore à quatre dimensions.
Toutes ces formes sont appelées polytopes, nous pouvons donc définir un polyèdre comme un polytope tridimensionnel. Le polyèdre est tout corps délimité, limité par un nombre fini de surfaces planes. On montre que les surfaces plates qui limitent un polyèdre sont des polygones.
Un polyèdre convexe est un polyèdre P, qui est à son tour un ensemble convexe; c'est-à-dire que s'il contient deux points A et B, il inclut le segment qu'ils déterminent.
Le polychore est une figure géométrique à 4 dimensions composée de plusieurs polyèdres.
Dénomination des polyèdres
Les polyèdres sont nommés en fonction de leur nombre de faces. La désignation est basée sur le grec classique. Par exemple, tétraèdre (4 faces), pentaèdre (5), hexaèdre (6, cube), heptaèdre (7), octaèdre (8), nonaèdre (9), décaèdre (10)... icosaèdre (20), etc.
Fréquemment, un polyèdre est qualifié par une description du type de faces qu'il contient. Si toutes leurs faces sont égales et que tous les angles de polyèdre sont égaux, on les appelle des polyèdres réguliers ou holoèdres (homoèdres). Par exemple, le dodécaèdre régulier ou le dodécaèdre pentagonal par rapport au dodécaèdre rhombique qui est hémièdre.
D'autres dénominations courantes indiquent qu'une opération a été réalisée dans un polyèdre plus simple qui l'a transformé en un polyèdre actuel. Par exemple, le cube tronqué, qui ressemble à un hexaèdre (cube) avec ses coins tronqués ou découpés. Il a donc 14 faces, et dans ce cas il n'est pas régulier car de ses faces, six ont la forme d'un octogone régulier et huit du triangle équilatéral. Ex. : le diploèdre à 24 faces.
Critères de classification des polyèdres
Les polyèdres peuvent être classés en plusieurs groupes selon leur famille d'origine ou les caractéristiques qui les différencient. selon leurs caractéristiques, ils se distinguent :
- Les convexes, comme le cube ou le tétraèdre, lorsqu'une paire de points dans l'espace se trouvant à l'intérieur du corps est jointe par un segment de ligne également interne. Au cas où ledit segment quitterait le corps, il s'agirait de polyèdres concaves, tels que le tore à facettes et les solides de Karim.
- Polyèdre à faces régulières, lorsque toutes les faces du polyèdre sont des polygones réguliers.
- Polyèdre à faces uniformes, lorsque toutes les faces sont égales.
- On parle de polyèdre à bords uniformes lorsque les paires de faces qui se rencontrent dans chaque bord sont égales.
- Polyèdre de sommets uniformes lorsque, dans tous les sommets du polyèdre, un même nombre de faces convergent et dans le même ordre.
- Polyèdre homoèdre (holoèdre) régulier ou régulier et uniforme, tel que le tétraèdre ou l'icosaèdre, quand il s'agit de faces régulières, de faces uniformes, de sommets uniformes et de bords uniformes.
Synonymes, antonymes
Voir tous les synonymes pour "polyèdre".1 synonyme (sens proche) de "polyèdre" :
- polytope tridimensionnel
0 antonyme (sens contraire).
Les mots ou les expressions apparentés à POLYÈDRE sont des termes qui sont directement liés les uns aux autres par leur signification, générale ou spécifique.
Le mot POLYEDRE est dans la page 7 des mots en P du lexique du dictionnaire.
Mots en P à proximité
polychrome polychromie polycondensation polyculture polydrupe polyèdrepolyélectrolyte polyènepolygame polygamie Polygonacées
En rapport avec "polyèdre"
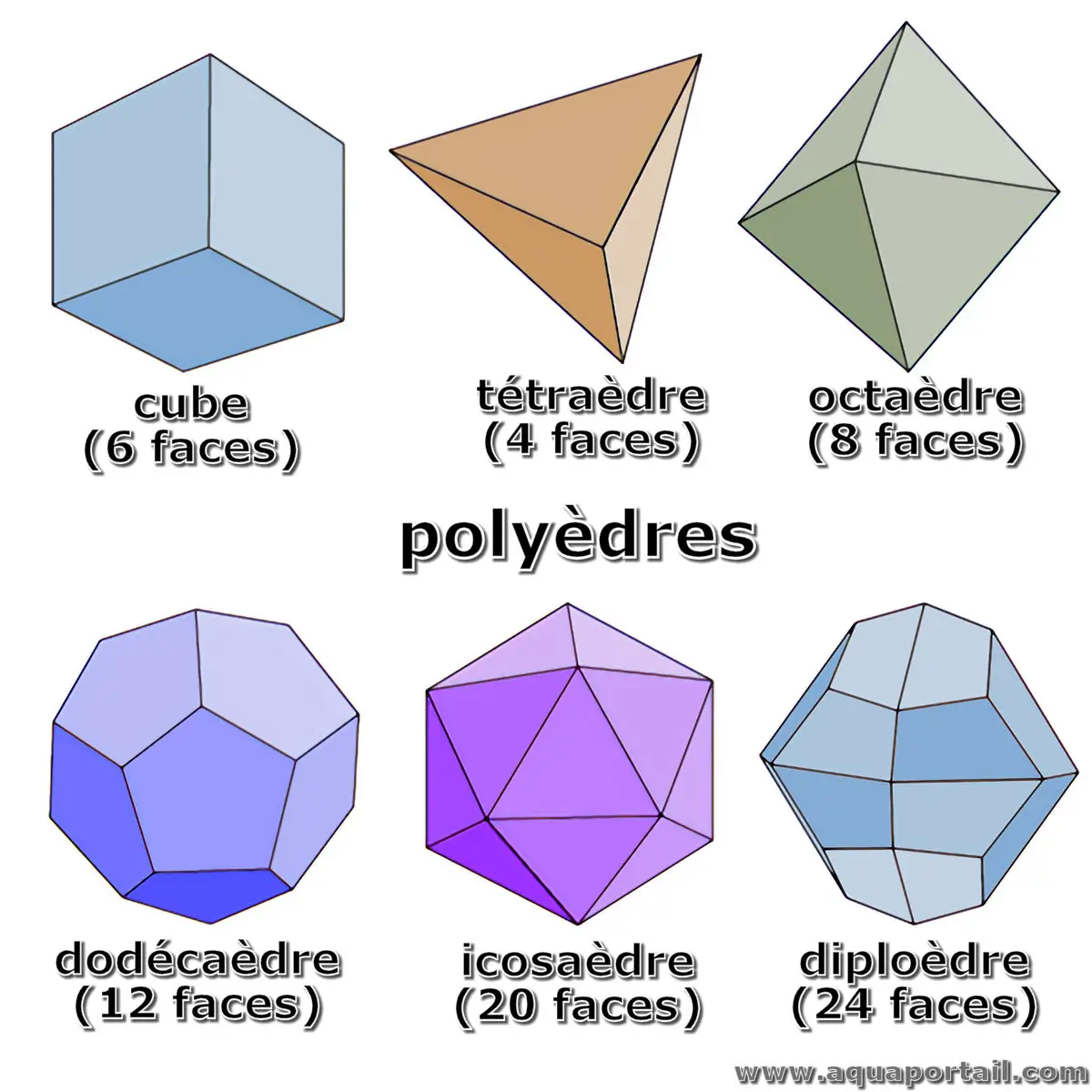
Un diploèdre est un polyèdre à 24 faces, une forme de double dodécaèdre. Les faces sont du type quadrilatère ou trapézoïdal. Le polyèdre est simplement...
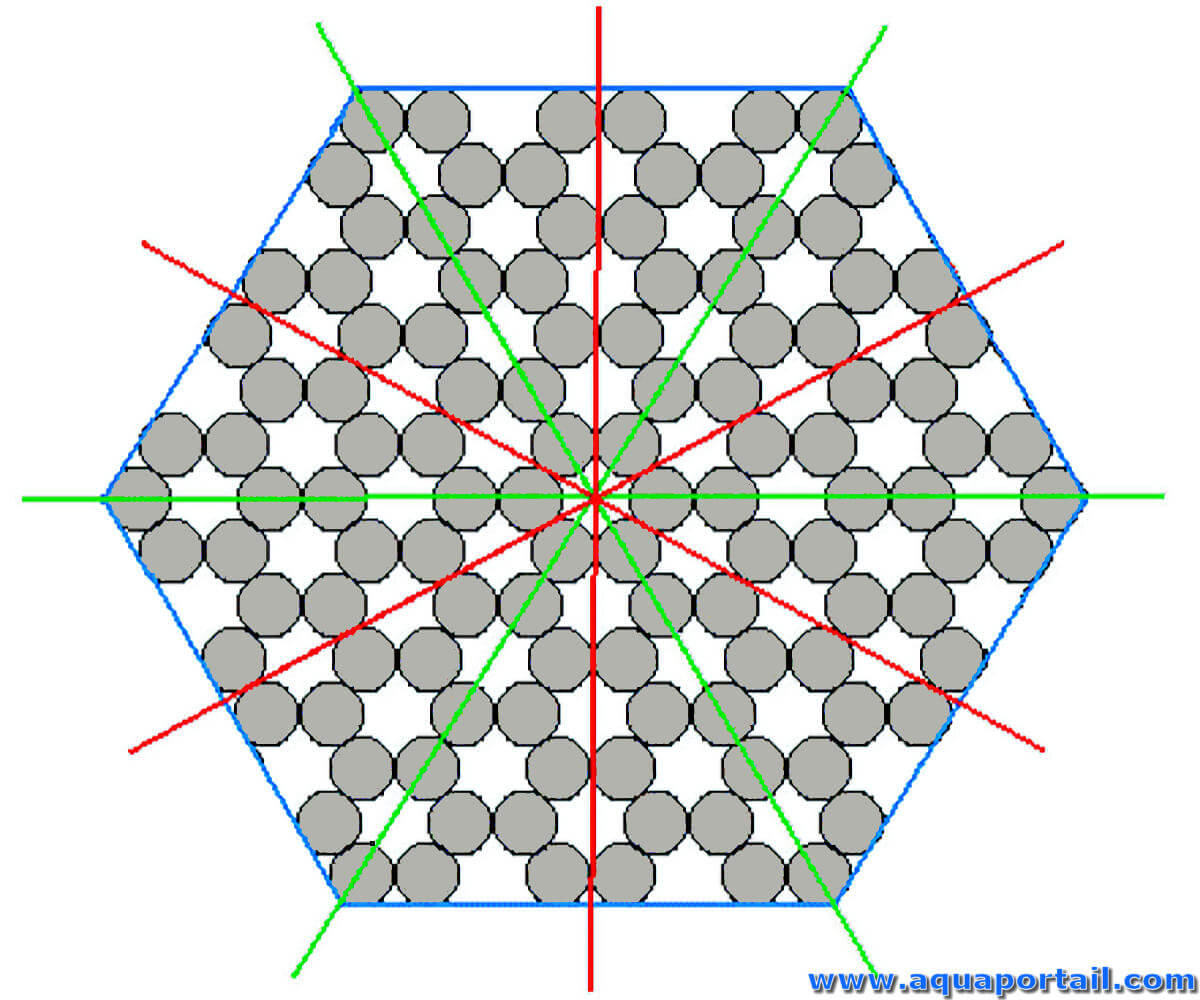
Ce qui est hémièdre présente les caractères de l'hémiédrie chez les polyèdres, notamment dans un solide dérivé d'un cristal.

En cristallographie, Un holoèdre, ou un homoèdre, est un cristal présentant une parfaite symétrie de ses faces, par opposition à un hémièdre...
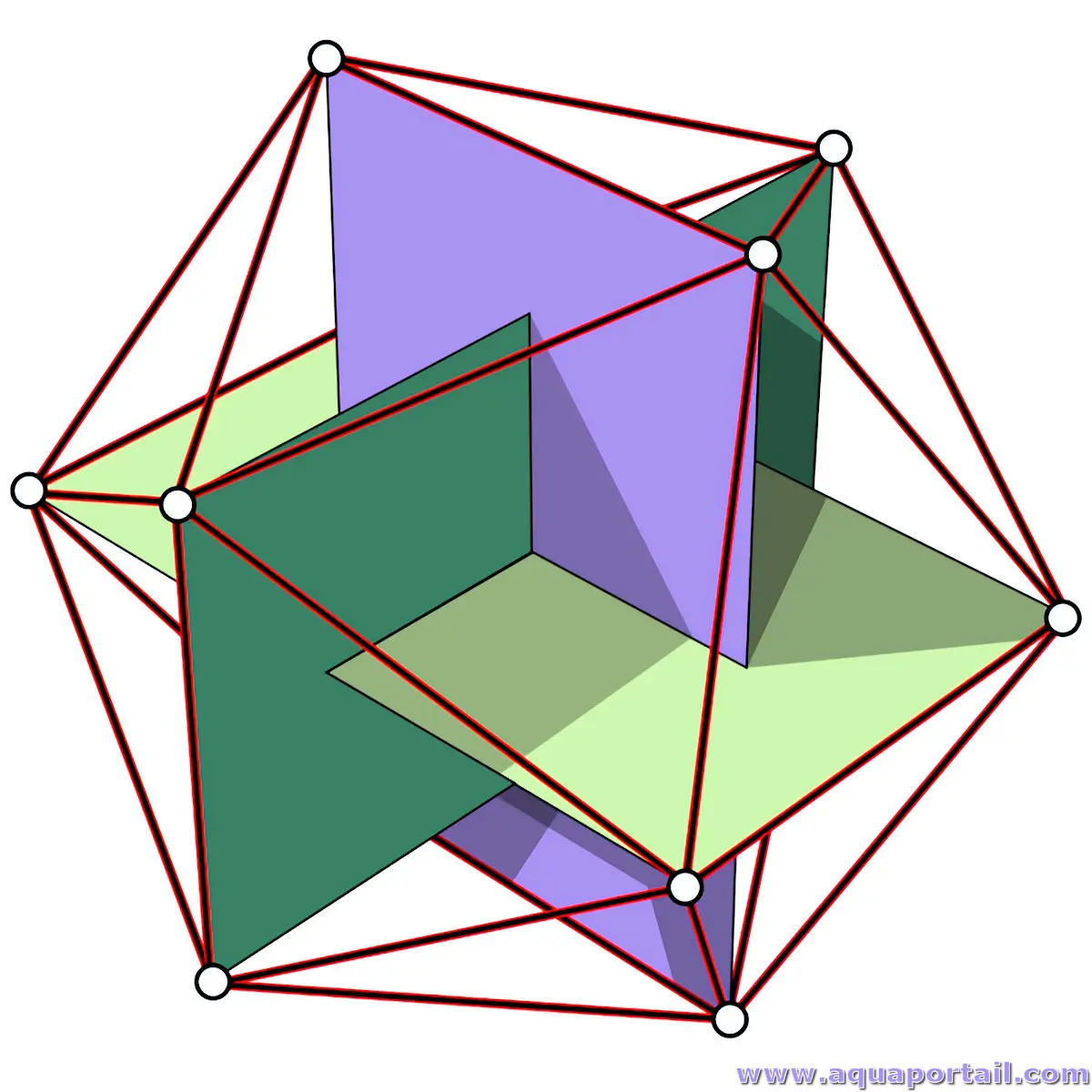
Un icosaèdre est une forme géométrique à 20 côtés, chacun composé d'un triangle équilatéral.
