Loi de Hardy-Weinberg

Définition

La loi de Hardy-Weinberg est la base de la génétique des populations. Elle postule qu'au sein d'une population panmictique, il existe un équilibre des fréquences alléliques et génotypiques d'une génération à l'autre.

La loi de Hardy-Weinberg définit un principe de distribution génotypique selon lequel, dans une population panmictique, illimitée, sans mutation et sans dérive génétique, et pour un gène à deux allèles A (fréquence p) et a (fréquence q), les 3 génotypes possibles AA, aa, Aa se stabilisent à la première génération avec les fréquences p² pour AA, q² pour aa et 2pq pour Aa. Cela respecte la méthode des carrés de Punnett en hérédité.

La loi d'équilibre de Hardy-Weinberg :

La loi (principe, équilibre) de Hardy-Weinberg pour deux allèles est représenté par deux courbes : l'axe horizontal montre les deux fréquences d'allèles p et q et l'axe vertical montre les fréquences de génotype attendues. Chaque ligne montre l'un des trois génotypes possibles. En incrustation, le schéma montre que la longueur de p, q correspond aux fréquences des allèles (ici p = 0,6, q = 0,4). Alors l'aire du rectangle représente les fréquences du génotype (donc AA : Aa : aa = 0,36 : 0,48 : 0,16).

Explications

La règle d'équilibre Hardy-Weinberg, d'après le mathématicien G. H. Hardy (1877–1947) et le médecin et chercheur en hérédité Wilhelm Weinberg (1862–1937), est un concept de génétique des populations. La loi est aussi appelée équation de Hardy-Weinberg, équilibre de Hardy-Weinberg, principe de Hardy-Weinberg, ou encore règle de Hardy-Weinberg.

Pour calculer ce modèle mathématique, on suppose une population idéale qui ne peut être trouvée dans la réalité. Cela signifie qu'il n'y a pas d'évolution car il n'y a pas de facteurs d'évolution qui pourraient changer le pool génétique. Dans ce cas, pour toute distribution génotypique de la génération parente, il existe une distribution génotypique de la première génération fille qui ne dépend que des fréquences alléliques et ne change pas dans les générations suivantes. Mathématiquement, cet équilibre est un point fixe de la fonction définie par le mécanisme d'héritage.

Malgré son caractère de modèle, l'équilibre Hardy-Weinberg est utilisé pour dériver les aspects génétiques des populations du modèle à la réalité. Ce modèle peut être utilisé de manière réaliste, en particulier pour des populations relativement importantes. La règle est également utilisée pour calculer la proportion d'individus hétérozygotes (ici dans l'exemple : Aa) dans l'hérédité récessive dominante, car les organismes hétérozygotes ne peuvent pas être distingués phénotypiquement de l'homozygote dominant (ici : AA) parce que l'allèle dominant prévaut.

Les lois mendéliennes ont été redécouvertes en 1 900, cependant, elles étaient encore doutées pendant quelques années car aucune déclaration n'a été faite sur la façon dont une génération de successeurs stables pourrait en résulter. Udny Yule s'est opposé à la demande en 1902 parce qu'il pensait que les allèles dominants devraient s'étaler dans le temps dans la population. L'Américain William Ernest Castle a montré en 1903 que les fréquences génotypiques restaient stables sans sélection. Carl Pearson, connu aujourd'hui pour ses contributions aux statistiques, a trouvé un point d'équilibre à p = q = 0,5 en 1903.

Description et modèle mathématique

La loi de Hardy-Weinberg répond à la question : Comment se fait-il que si une mutation est dominante, nous ne sommes pas tous sujets à cette mutation ? Punnett a posé cette question à Hardy, un mathématicien anglais renommé, qui après peu de temps a trouvé la solution.

Il a simplifié le problème en indiquant qu'il n'y avait pas d'influences extérieures et a conclu que la liberté qui se manifestait dans la mutation avait essentiellement deux conséquences :

• les fréquences des allèles dans une population examinée sont restées constantes;
• les fréquences relatives des différents génotypes resteraient les mêmes après la première génération.

Hardy et le médecin allemand Weinberg ont formulé indépendamment cette formule mathématique : p² + 2pq + q² = 1, ou de manière équivalente : (p+q)² = 1. Ceci est valable dans le cas simple du locus unique avec deux allèles "A" et "a", avec deux fréquences de type f(A)=p et f(a)=q.

Les génomes que nous attendons sont donc :

• f(AA) = p², probabilité qu'un ovule contenant l'allèle "A" rencontre un spermatozoïde contenant "A".
• f(Aa) = 2pq, la somme de la probabilité qu'un ovule avec l'allèle "A" rencontre un gamète mâle contenant "a" et la probabilité qu'un gamète femelle avec "a" rencontre un spermatozoïde ayant "A".
• f(aa) = q², probabilité qu'un gamète mâle et un gamète femelle, tous deux avec l'allèle "a", se rencontrent.

La loi de H-W décrit la situation la plus simple d'équilibre génétique d'une population : bien que les conditions de l'équilibre de Hardy-Weinberg semblent difficiles à obtenir, elles s'appliquent à de nombreux caractères dans plusieurs situations.

Les conditions dans lesquelles un locus dans une population suit la loi de H-W sont les suivantes :

• HW1 : population pratiquement infinie. Ceci est nécessaire pour que la loi des grands nombres soit appliquée, et donc les fréquences sont pratiquement coïncident avec les probabilités. Étonnamment, une population de quelques centaines d'individus suffit, alors que des fluctuations sont possibles (mais peu probables).
• HW2 : absence d'immigration et d'émigration. De cette façon, le pool génétique n'est influencé que par sa dynamique interne.
• HW3 : panmixie (croisement aléatoire). Cela signifie que la probabilité de croisement de deux individus n'est pas affectée par le phénotype du personnage en question. De cette façon, c'est comme si les gènes de tous les individus étaient mélangés dans le pool génétique et extraits par tirage au sort pour créer les génotypes des nouveaux individus. La panmixie est absente, par exemple, dans le cas de fortes préférences de mariage au sein de castes fermées, surtout si elles ont une origine ethnique différente.
• HW4 : pas de sélection. Le succès reproductif moyen des individus (également appelé fitness) ne doit pas être affecté par le génotype du personnage en question. Les deux (ou plusieurs) allèles doivent donc avoir la même probabilité, une fois présents, d'être transmis aux générations suivantes.
• HW5 : non-mutation. De toute évidence, les mutations modifient la composition du pool génétique des nouvelles générations. Cependant, ce sont des événements rares.

L'équation de Hardy-Weinberg stipule que dans les conditions ci-dessus, les fréquences des gènes restent constantes et les fréquences génotypiques se stabilisent en une génération de sorte que la fréquence des homozygotes est le carré de celle de l'allèle, tandis que celles des hétérozygotes seront le double produit des fréquences des allèles possédés.

Origine

G. H. Hardy, un mathématicien britannique, et W. Weinberg, un médecin allemand, ont réalisé qu'ils pouvaient appliquer une approche similaire pour prédire le résultat d'un accouplement aléatoire, non seulement pour un croisement individuel, mais pour les croisements intervenant au sein d'une population entière.

Après tout, la combinaison aléatoire de gamètes, telle qu'étudiée par Mendel pour des croisements individuels, est assez similaire dans son concept à l'accouplement aléatoire de génotypes. Dans un croisement individuel, c'est une question de hasard quel spermatozoïde se combinera avec quel ovule.

Dans une population infiniment grande, qui s'accouple au hasard, c'est une question de chance que les génotypes se combinent. La détermination de la distribution des fréquences de génotype dans une population d'accouplement aléatoire peut également être réalisée à l'aide d'un carré de Punnett. Cependant, plutôt qu'un seul croisement entre deux parents, Hardy et Weinberg ont examiné des croisements entre toutes les mères et tous les pères d'une population.

Considérations

L'équation de Hardy-Weinberg a été dérivée pour un ensemble strict de conditions. Il suppose que la population est en équilibre, c'est-à-dire qu'elle ne subit aucun changement net dans la fréquence des allèles au fil du temps. Pour atteindre l'équilibre, les conditions suivantes doivent être remplies :

1. accouplement aléatoire;
2. une population infiniment nombreuse;
3. pas de mutation;
4. pas de migration vers ou hors de la population;
5. pas de sélection des génotypes (tous les génotypes sont également viables et également fertiles).

En réalité, bien sûr, il n'y a pas de populations qui répondent à ces exigences. Néanmoins, la plupart des populations raisonnablement importantes se rapprochent de ces conditions dans la mesure où l'équation de Hardy-Weinberg peut être appliquée pour estimer les fréquences génotypiques.

En rapport avec "loi de Hardy-Weinberg"

• carré de Punnett

  

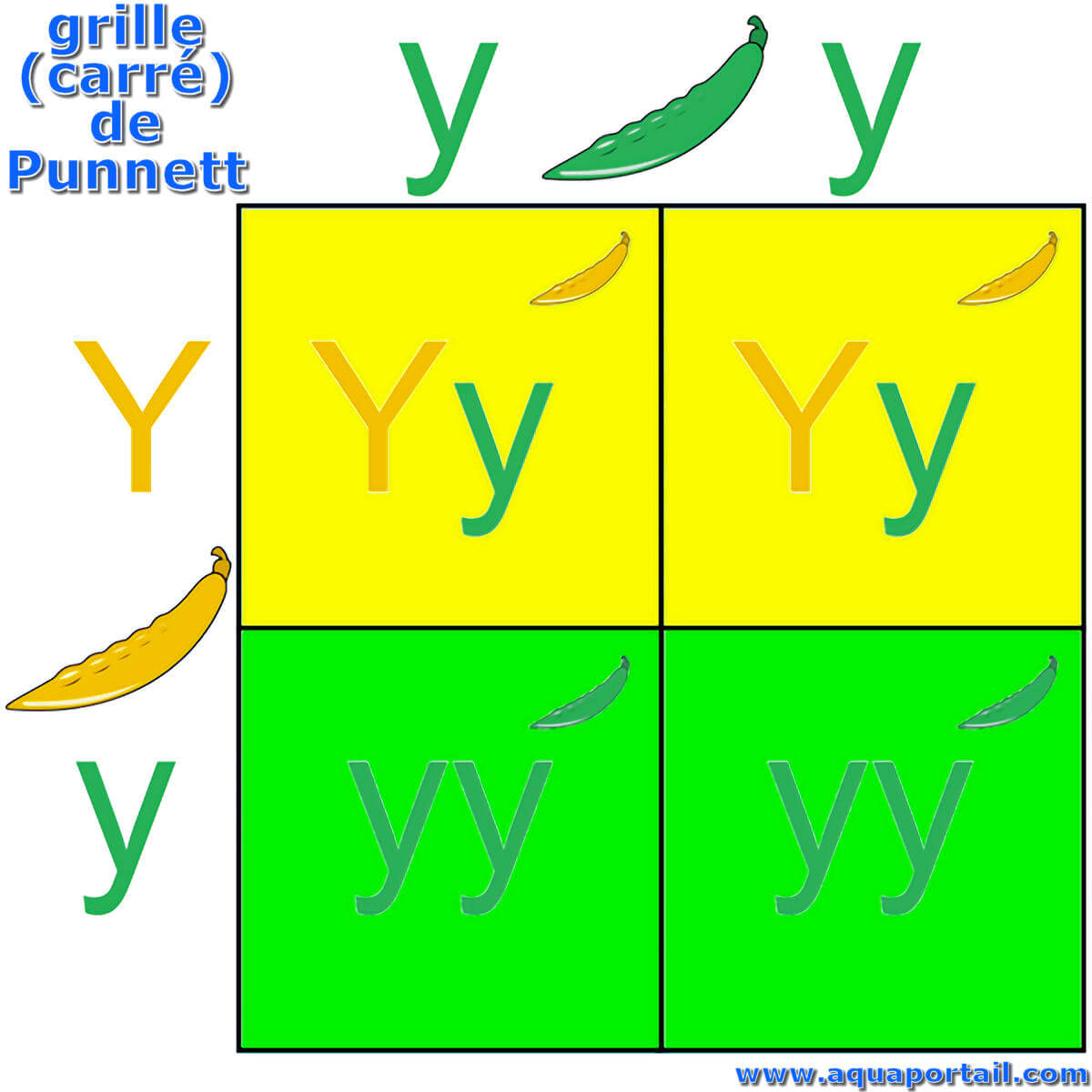
  Le carré de Punnett est un tableau en damier dans lequel sont donnés tous les résultats possibles d'un croisement génétique entre deux individus de génotypes...

• fréquence allélique

  

  Une fréquence allélique est la fréquence d'un allèle par rapport à celle d'autres allèles du même gène dans une population.

• hérédité

  

  L'hérédité est la transmission des caractères héréditaires d'un individu à ses descendants par l'intermédiaire de ses gènes.

• loi de Haeckel

  

  La loi de Haeckel, ou la théorie de la récapitulation, est une loi biogénétique de parallélisme embryologique qui part du principe selon lequel l'ontogenèse...