Sphérique
Définition
Est sphérique toute forme apparentée à une sphère comme une boule, un ballon ou un globe (orbe). Est admis sphérique ce qui est relatif à ou traitant d'une sphère ou de ses propriétés.
Quelque chose de sphérique est comme une sphère en étant rond, ou plus ou moins rond, en trois dimensions. Ex. : les pommes et les oranges sont toutes deux sphériques, même si elles ne sont jamais parfaitement rondes.
Une boule sphérique :
Une boule parfaite géométriquement sphérique. Le diamètre d'une sphère est égal en tous points. Un triangle sphérique est composé de trois arcs de grands cercles, comme dans l'image ci-dessus. Si c'était la Terre, vous pourriez imaginer commencer par le pôle Nord, suivre 0 degré de longitude jusqu'à l'équateur (indiqué en jaune), suivre l'équateur jusqu'à 30 degrés de longitude est, puis suivre cette ligne de longitude jusqu'au pôle Nord.
Explications
Si un objet est gros, largement visible à l'oeil nu, il est qualifié de macrosphérique; à l'inverse, s'il est microscopique et non visible à l'oeil nu, il est microsphérique.
Sphéroïde
Un sphéroïde a une forme à peu près sphérique; Ainsi, un astéroïde, par exemple, est souvent sphéroïdal, assez rond, mais grumeleux.
Macrosphérique
Ce qui est macrosphérique est en rapport avec une macrosphère, une sphère visible à l'oeil nu, relativement large (dans des contextes variés).
Un animal macrosphérique, chez les foraminifères, se dit de la loge sécrétée par les schizozoïtes et constituant la loge initiale du gamonte.
La mousse syntactique macrosphérique intègre de plus grandes sphères renforcées de fibres (diamètre moyen de 5 mm) dans la structure syntaxique, atteignant ainsi des densités plus faibles dans certaines applications. Idéalement adaptée à la fabrication de tailles standard plus grandes et de structures personnalisées, la mousse syntactique macrosphérique équivaut généralement à une flottabilité à moindre coût pour une profondeur donnée.
Géométrie
La géométrie sphérique est tout simplement la géométrie d'une sphère. Ici, une sphère est un ensemble de points équidistants d'un centre donné.
D'un point de vue euclidien, il y a des points sur la sphère, mais évidemment pas de lignes droites. En géométrie sphérique, nous définissons un point comme étant une paire de points antipodaux sur la sphère et une ligne comme étant un grand cercle sur la sphère. Il en résulte deux jolis théorèmes de géométrie sphérique : deux lignes distinctes déterminent (se croisent) un seul point, et deux points distincts déterminent une seule ligne.
Ceci s'écarte de la géométrie euclidienne, car cela signifie qu'il n'y a pas de lignes parallèles dans la géométrie sphérique, puisque des lignes distinctes se coupent toujours.
Considérez la déclaration "Deux lignes distinctes déterminent un seul point". Effectuez maintenant le remplacement simple suivant : remplacez l'occurrence de "Ligne" par "Point" et vice versa. Cela donne la déclaration "Deux points distincts déterminent une seule ligne" et est appelée le dual de la déclaration originale.
Ainsi, nous nous trouvons dans une situation où une affirmation et son dual sont tous deux vrais. Maintenant, si cela est vrai pour un ensemble d'énoncés en géométrie sphérique – que le dual de chaque énoncé est vrai – et que nous tirons un nouveau résultat de cet ensemble d'énoncés, alors la chose remarquable suivante intervient. Puisque le dual de toute affirmation que nous avons utilisée est vrai, alors le dual du nouveau résultat doit également être vrai ! Remplacez simplement chaque instruction utilisée pour dériver le nouveau résultat par son dual, et vous obtenez également le dual du nouveau résultat comme une instruction vraie.
C'est le principe de dualité en mathématiques et c'est un concept très important. Nous le retrouverons lorsque nous étudierons la géométrie projective.
Les triangles et la trigonométrie sont également différents sur la sphère.
Sur la sphère, cependant, les côtés d'un triangle sont en réalité des angles. Bien sûr, vous pouvez mesurer la longueur des arcs en fonction du rayon de la sphère, mais ce n'est pas aussi utile.
Synonymes, antonymes
Voir tous les synonymes pour "sphérique".8 synonymes (sens proche) de "sphérique" :
1 antonyme (sens contraire) :
- cubique
Les mots ou les expressions apparentés à SPHÉRIQUE sont des termes qui sont directement liés les uns aux autres par leur signification, générale ou spécifique.
Le mot SPHERIQUE est dans la page 4 des mots en S du lexique du dictionnaire.
Mots en S à proximité
Sphagnopsidées sphaigne sphalérite sphénoïde sphénotique sphériquesphéroblaste sphéroplaste sphincter sphyrène spicastre
En rapport avec "sphérique"
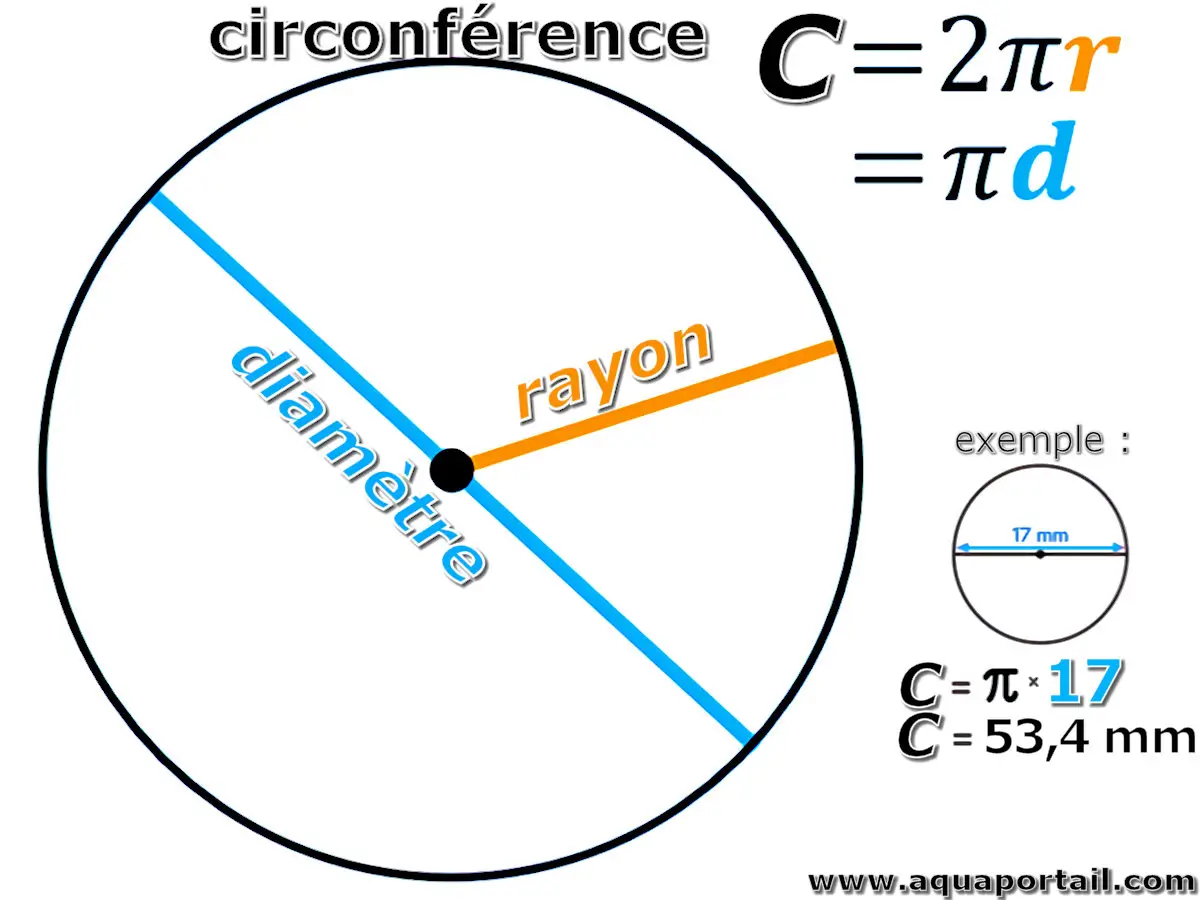
La circonférence est la valeur de longueur du périmètre d'un cercle ou d'une forme ovale (ellipse).

Est convexe toute forme qui se courbe vers l'extérieur, comme un ballon de rugby. Son opposé est concave. La ligne convexe se courbe vers l'extérieur...

Est globuleux ce qui a une forme plus ou moins sphérique comme celle d'un globe, d'une sphère, d'un globule.

Ce qui est orbiculaire dispose d'un contour presque circulaire, rond, sphérique. Une forme orbiculaire ressemble à un cercle, ayant la forme d'un anneau plat...
